Publications and Preprints

Research topics: analytic number theory, spectral theory of automorphic forms, hyperbolic lattice point counting, Prime Geodesic Theorems, Quantum Unique Ergodicity, Zeta and Dirichlet L-functions.

  1. On the variance of the nodal volume of arithmetic random waves, joint with G. Cherubini, Forum Math., 2021  (advance publication)
  2. Second moment of the prime geodesic theorem for \mathrm{PSL}(2, \mathbb{Z}[i]), joint with D. Chatzakos and G. Cherubini, Math. Z., 2021 (advance publication)
  3. Bykovskii-type theorem for the Picard manifold, joint with A. Balog, A. Biró and G. Cherubini, Int. Math. Res. Notices, 2020 (advance publication)
  4. Prime geodesic theorem in the 3-dimensional hyperbolic space, joint with O. Balkanova, D. Chatzakos, G. Cherubini and D. Frolenkov, Trans. Amer. Math. Soc., 372, no. 8, 2019, pp. 5355-5374
  5. Quantum limits of Eisenstein series in 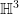\mathbb{H}^{3}, Probabilistic methods in geometry, topology and spectral theory, pp. 125-138, Contemp. Math., 739, Amer. Math. Soc., Providence, RI, 2019
  6. On the value distribution of two Dirichlet 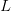L-functions, joint with Y. Petridis, Funct. Approx. Comment. Math., 58, no. 1,  2018, pp. 43-68
  7. Lattice point counting in sectors of hyperbolic 3-space, Q. J. Math, 68, issue 3, 2017, pp. 891-922
  8. Numerical Investigation of Exponential Sums Over Eigenvalues in 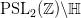\mathrm{PSL}_{2}(\mathbb{Z})\backslash\mathbb{H}, appears in Local average in hyperbolic lattice point counting, with an Appendix by Niko Laaksonen in Math. Z., 285, issue 3-4, 2017, pp. 1319-1344
    (see here for a discussion on the numerics, and links to the programs and data)
  9. Discrete mean values of Dirichlet 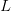L-functions, joint with Y. Petridis, The Analytic Theory of Automorphic Forms, Oberwolfach Report, 8, no. 3, 2011

My doctoral thesis “Quantum Limits, Counting and Landau-type Formulae in Hyperbolic Space“,
and master’s thesis “Discrete Mean Values of Dirichlet 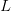L-functions“.